
Zadanie Układy scalone (ukl)
Pomóż nam usprawnić bazę zadań!
Układy scalone
Limit pamięci: 32 MB
Układy scalone produkowane przez Bajtocką Fabrykę Elektroniczną
mają postać półprzewodnikowych płytek, na których znajdują się tranzystory.
Końcówki niektórych par tranzystorów połączone są za pomocą
specjalnych mikrodrucików, które przewodzą prąd tylko w jedną stronę
i charakteryzują się różnymi wartościami impedancji (jest to bardziej
zaawansowana forma oporu).
Jakość układu scalonego mierzy się w fabryce jako liczbę występujących
w nim różnych ścieżek o impedancji równej dokładnie  .
.
Ścieżką w układzie nazywamy dowolny sposób przejścia między jednym tranzystorem układu a drugim z użyciem mikrodrucików (drugi tranzystor może być tym samym, co pierwszy), w której nie przemieszczamy się ani razu po mikrodruciku w kierunku przeciwnym do kierunku przewodzenia przez niego prądu. Każda ścieżka musi zawierać co najmniej jeden mikrodrucik. Ścieżka może przechodzić przez każdy tranzystor i mikrodrucik dowolnie wiele razy. Impedancję ścieżki liczy się jako iloczyn impedancji mikrodrucików na niej występujących.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis układu scalonego, liczby
 oraz
oraz  ,
,
- wyznaczy resztę z dzielenia przez
 liczby
ścieżek w układzie scalonym o impedancji
liczby
ścieżek w układzie scalonym o impedancji  ,
,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera cztery liczby całkowite dodatnie
 ,
,  ,
,  oraz
oraz  (
( ,
,  ,
,
 ,
,  ), pooddzielane pojedynczymi odstępami.
Gdzie odpowiednio
), pooddzielane pojedynczymi odstępami.
Gdzie odpowiednio  oznacza liczbę tranzystorów w układzie,
oznacza liczbę tranzystorów w układzie,
 liczbę mikrodrucików,
liczbę mikrodrucików,  impedancję poszukiwanch ścieżek,
a
impedancję poszukiwanch ścieżek,
a  liczbę, przez którą będziemy dzielili z resztą.
Kolejnych
liczbę, przez którą będziemy dzielili z resztą.
Kolejnych  wierszy zawiera po trzy liczby całkowite dodatnie
wierszy zawiera po trzy liczby całkowite dodatnie
 ,
,  i
i  (
( ,
,  ,
,
 ), pooddzielane pojedynczymi odstępami i oznaczające
mikrodrucik o impedancji
), pooddzielane pojedynczymi odstępami i oznaczające
mikrodrucik o impedancji  , przewodzący prąd z tranzystora o numerze
, przewodzący prąd z tranzystora o numerze
 do tranzystora o numerze
do tranzystora o numerze  .
Żadna para uporządkowana
.
Żadna para uporządkowana  nie pojawi się na wejściu
więcej niż raz.
nie pojawi się na wejściu
więcej niż raz.
Wyjście
Pierwszy i jedyny wiersz wyjścia powinien zawierać albo jedno słowo
NIESKONCZONOSC, jeżeli płytka zawiera nieskończenie wiele
ścieżek o impedancji  , albo resztę z dzielenia
przez
, albo resztę z dzielenia
przez  liczby wszystkich takich ścieżek, jeżeli ich liczba
jest skończona.
liczby wszystkich takich ścieżek, jeżeli ich liczba
jest skończona.
Przykład
Dla danych wejściowych:
4 6 6 1000 2 1 3 1 3 2 1 4 2 4 2 4 4 3 3 3 4 2

5
natomiast dla danych wejściowych:
4 4 1 1000 2 1 1 4 2 1 3 4 1 1 3 1
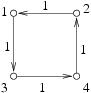
poprawnym wynikiem jest:
NIESKONCZONOSC
W pierszym przykładzie wszystkimi ścieżkami o impedancji  są:
są:
-
 ,
,
-
 ,
,
-
 ,
,
-
 ,
,
-
 .
.
 ,
a wszystkich ścieżek w układzie jest nieskończenie wiele.
,
a wszystkich ścieżek w układzie jest nieskończenie wiele.
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English